How to Find HCF
A
Prime Number.
A prime number is a number greater than 1 and can be
divided by 1 and itself.
Even
Number- a number that can be divided by 2 that is remainder
is 0.
4,6,8.
Odd number
A number that cannot be divided by 2. The remainder is
not 0.
7,9,11
HCF
is the most common Factor
What is the highest common Factor?
The largest whole numbers are shared by two given
numbers.
For example 5, 10.
How
to find HCF?
Find HCF of 4, 6.
The factors are 1, and
2, 5 for both.
5
is called HCF
List
the factors of each and find common.
4:1,
2,
4
6:1, 2, 3, 6
Highest common factor is 2.
Venn diagram
12 30
2 2 5
3
HCF=6
One
way to solve HCF is prime Factorization
Method:
1. Tree
Method
2. Division
Method
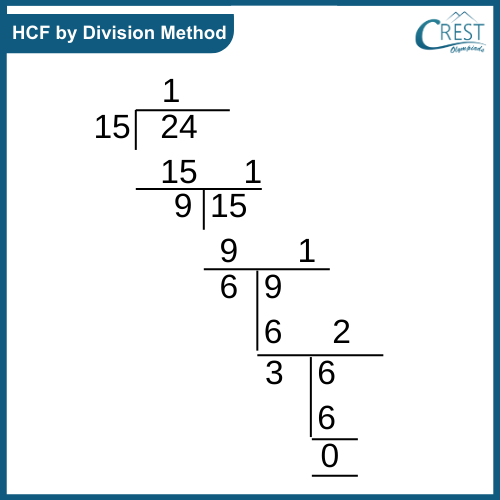
The
Division Method.
Divide by the smallest prime number until the Quotient
is 1.
HCF is the product of common prime factors with the smallest
powers.
Tree
method
Find it out. Homework
Algebraic
Equation
1.
Linear Equation- They have two variables and will not have exponentials.
Example
ax+by+c.
2.A
quadratic equation is a polynomial equation of the second
degree.
3.
A cubic equation is a
polynomial equation of the third degree in which there are three 'x' variables
with one that is raised to the third power, one raised to the second power, and
one that does not have an exponent.
Solving
quadratic equation
Middle
Term
Number 1=a, number 2=b
·
Product of two numbers =ac
·
Sum is equal=b.
Why we have not used middle Term?
Quadratic Formula
x=
Algebraic
Identities
·
(a + b)2 = a2 + 2ab + b2
- (a - b)2 = a2 - 2ab + b2
- (a + b)(a - b) = a2 - b2
- (x + a)(x + b) = x2 + x(a
+ b) + ab
Problem
Let's compute \(h(g(f(x))))\) step by step using the
provided functions:
Given:
\[h(x) = x^2 + 1\]
\[g(x) = x + 4\]
\[f(x) = 1 - 2x\]
First, find \(g(f(x))\):
\[g(f(x)) = g(1 - 2x)\]
\[g(f(x)) = (1 - 2x) + 4\]
\[g(f(x)) = 5 - 2x\]
Now, find \(h(g(f(x)))\):
\[h(g(f(x))) = h(5 - 2x)\]
\[h(g(f(x))) = (5 - 2x)^2 + 1\]
\[h(g(f(x))) = 25 - 20x + 4x^2 + 1\]
\[h(g(f(x))) = 4x^2 - 20x + 26\]
The given equation is \(h(g(f(x))) = 4x^2 + px + q\).
Comparing coefficients:
From \(h(g(f(x))) = 4x^2 - 20x + 26\), the coefficient
of \(x\) term is \(-20x\). To match this with \(px\), \(p\) must be \(-20\).
Additionally, the constant term in \(h(g(f(x)))\) is
\(26\), which matches with \(q\) in the equation. Therefore, \(q = 26\).
Therefore, the values of \(p\) and \(q\) are \(p =
-20\) and \(q = 26\).
Pls like us in FB.